What is yielding in Finite Element Analysis?

What is yielding?

Yielding refers to the deformation of a material beyond its elastic limit under applied stress, leading to permanent or plastic deformation. When a material is subjected to stress, it initially deforms elastically, meaning it returns to its original shape once the stress is removed. However, if the applied stress exceeds a certain threshold known as the yield strength, the material undergoes plastic deformation, and it does not return to its original shape upon the removal of the stress.

Yielding typically occurs in ductile materials, such as metals, where the atomic structure allows for significant atomic rearrangement without fracturing. During yielding, the material undergoes permanent deformation as dislocations within its crystal lattice move and rearrange, resulting in the material taking on a new shape. This plastic deformation is irreversible and can lead to changes in the mechanical properties of the material, such as increased ductility or reduced strength.

Yielding is an essential consideration in engineering design and structural analysis, as it influences the behavior and performance of materials under load. Understanding the yield behavior of materials is crucial for designing structures and components that can withstand the stresses and strains they are subjected to during operation without experiencing failure or excessive deformation.

Main characteristics and variables in the behaviour of materials related to yielding

In materials science and engineering, yielding specifically refers to the point at which a material transitions from elastic deformation to plastic deformation under applied stress. Here's a breakdown of the key aspects:

• Elastic Deformation: When a material is subjected to stress within its elastic limit, it deforms elastically, meaning it returns to its original shape once the stress is removed. In this stage, the atoms or molecules within the material experience temporary displacement, but they do not permanently change their positions relative to each other.

• Yield Point: The yield point is the stress level at which the material begins to undergo plastic deformation. For some materials, this transition from elastic to plastic behavior is well-defined and marked by a distinct yield point on the stress-strain curve. However, not all materials exhibit a clear yield point, especially those with a more gradual transition from elastic to plastic behavior.

• Plastic Deformation: Once the yield point is reached, the material undergoes plastic deformation, meaning it experiences permanent changes in shape or size even after the applied stress is removed. In this stage, the atoms or molecules within the material undergo significant rearrangement, leading to the formation of dislocations and the onset of plastic flow.

• Yield Strength: The yield strength is the maximum stress a material can withstand without undergoing plastic deformation. It is a critical material property that indicates the material's resistance to yielding under load. Yield strength is typically determined through tensile testing, where the stress at which the material exhibits a specified amount of plastic deformation (e.g., 0.2% offset yield strength) is measured.

• Ductility and Toughness: Yielding is often accompanied by an increase in ductility, which is the ability of a material to deform plastically without fracturing. Materials that exhibit significant ductility can undergo extensive plastic deformation before failure, making them desirable for applications where deformation tolerance is important. Additionally, the toughness of a material, which is its ability to absorb energy without fracturing, may also be influenced by yielding behavior.

What is the Von Mises stress?

The Von Mises stress, also known as the equivalent stress or equivalent von Mises stress, is a measure used in solid mechanics to assess the combined effect of multiple stress components on a material's yielding behavior. It is particularly useful for predicting yielding in ductile materials subjected to complex stress states, where traditional stress measures like normal and shear stresses may not adequately represent the material's response. Here's an explanation of the Von Mises stress:

• Background: The Von Mises stress is based on the concept that yielding in ductile materials is primarily governed by the magnitude of the deviatoric (shear) stress components, rather than the hydrostatic (pressure) stress component. This is because the hydrostatic stress does not contribute to yielding in ductile materials, whereas the deviatoric stresses do.

• Mathematical Formulation: The Von Mises stress (σVM) is calculated using the individual stress components. For a three-dimensional stress state, the Von Mises stress is computed using the following equation:

            This equation accounts for the contributions of both normal stresses (σ) and shear                          stresses (τ) in all three principal directions.

• Interpretation: The Von Mises stress represents the equivalent stress that, if acting alone, would produce the same yielding behavior in a material as the actual combination of stresses present. It provides a single scalar value that can be compared to the material's yield strength to assess whether yielding is likely to occur. If the Von Mises stress exceeds the material's yield strength, yielding is predicted to occur.

• Applications: The Von Mises stress is widely used in engineering analysis and design, particularly in finite element analysis (FEA), where complex stress states are common. It enables engineers to assess the safety and reliability of structures and components subjected to multiaxial loading conditions, helping to prevent unexpected failures and optimize designs for maximum performance and durability.

Therefore, the Von Mises stress is a valuable tool in solid mechanics for predicting yielding in ductile materials under complex stress states, providing engineers with critical information for design and analysis purposes.

What is the Von Mises yield criterion?

The Von Mises yield criterion, also known as the Von Mises-Hencky yield criterion or simply the Von Mises criterion, is a mathematical formula used in materials science and solid mechanics to predict yielding or failure in ductile materials subjected to multiaxial stress states. It provides a criterion for determining when yielding occurs based on the stress components acting on a material.

The Von Mises yield criterion is derived from the concept that yielding in ductile materials is primarily controlled by the distortion or shear strain energy, rather than the individual normal and shear stresses. This criterion is widely used in engineering design and analysis to assess the safety and performance of structures and components under complex loading conditions.

The mathematical expression for the Von Mises yield criterion is as follows:

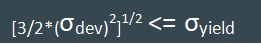
where σdev ​is the deviatoric (or equivalent) stres and σyield​ is the material's yield strength. σdev is calculated as:

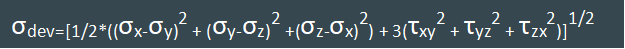
This represents the combined effect of normal and shear stresses on the material, excluding the hydrostatic (pressure) component.

According to the Von Mises criterion, yielding or failure occurs when the deviatoric stress exceeds the material's yield strength. In other words, if the Von Mises stress (σVM) is greater than or equal to the material's yield strength, then yielding is predicted to occur.

The Von Mises yield criterion is widely used in engineering analysis, particularly in finite element analysis (FEA), where complex stress states are common. It provides a convenient and accurate method for predicting yielding in ductile materials under multiaxial loading conditions, aiding in the design and optimization of structures and components for maximum performance and safety.