Why is dynamic FEA an essential aspect in engineering practice?

Types of dynamic loads

Seismic movements (earthquakes)
Seismic movements produce loads known as seismic or earthquake loads, caused by ground shaking due to tectonic activity. These loads result in inertial forces within structures as they resist sudden accelerations and displacements. The magnitude of seismic loads depends on the earthquake's intensity, the structure's mass, stiffness, and dynamic properties. These forces can cause vibrations, deformations, and, in extreme cases, collapse if not properly addressed. Designing for seismic loads is crucial to ensure structural safety and resilience during earthquakes.
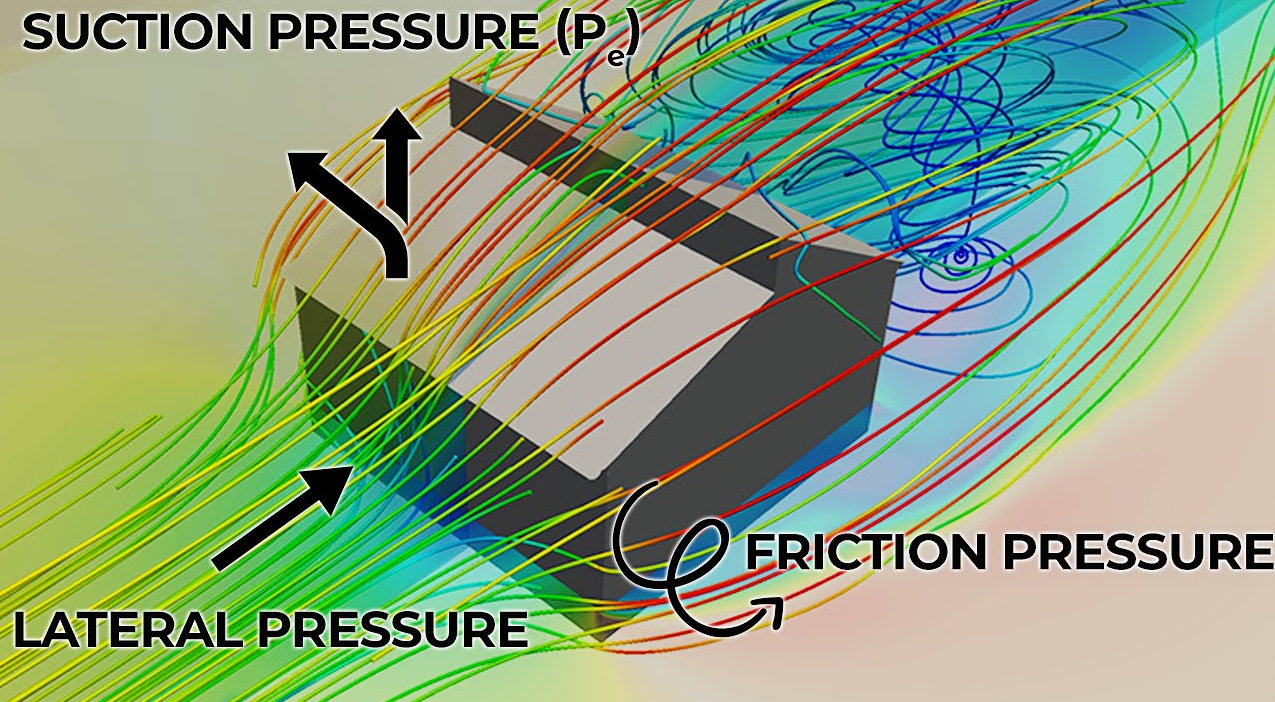
Wind action
Wind loads are forces exerted by the movement of air on structures and objects, caused by atmospheric pressure differences due to temperature variations, weather systems, or geographical factors. These loads depend on wind speed, air density, and the shape, size, and orientation of the structure. Buildings, bridges, towers, and other exposed structures experience wind loads, which can lead to vibrations, deflections, or structural failure if not properly accounted for. Factors like turbulence, gusts, and aerodynamic effects, such as lift and drag, influence the magnitude and distribution of wind loads. In engineering, wind loads are analyzed using standards and simulations to ensure structures can withstand both static and dynamic wind effects.

Wave action
Ocean currents generate loads on structures submerged or partially submerged in water, such as offshore platforms, pipelines, and ships. These loads arise from the continuous movement of water exerting drag, lift, and pressure forces on the structure. The magnitude of these forces depends on the current's speed, water density, and the structure's shape, size, and orientation. Marine current loads can cause vibrations, fatigue, and stability issues if not properly considered. Accurate analysis is essential for ensuring the durability and safety of marine and coastal structures.
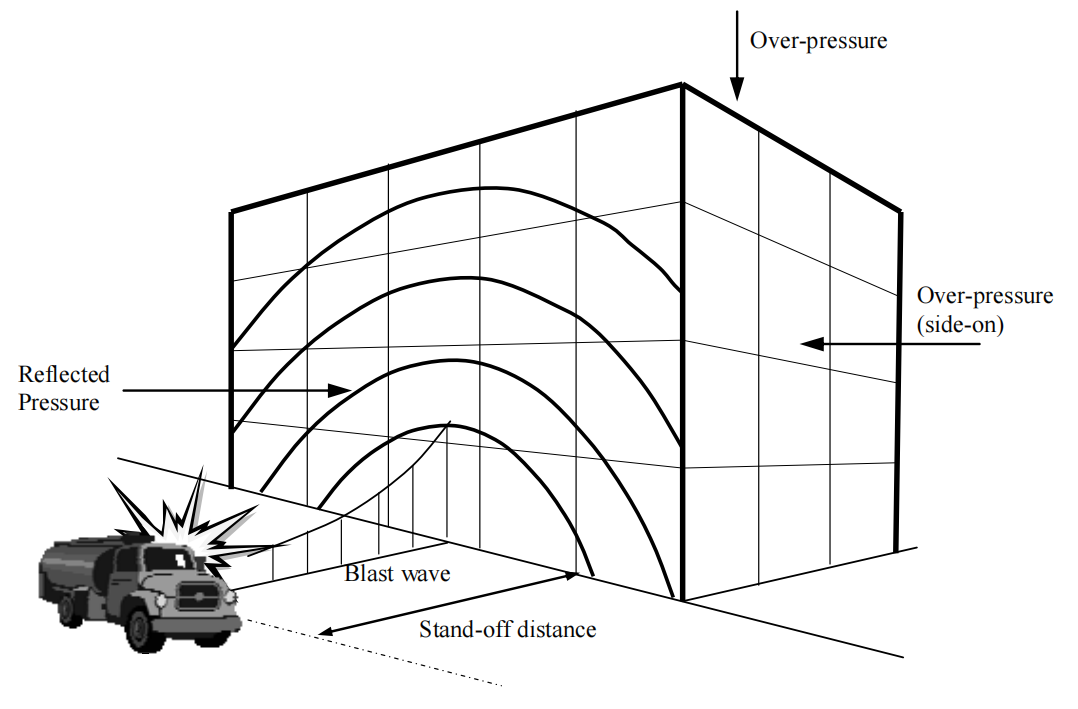
Explosions
Explosions generate loads known as blast loads, caused by the rapid release of energy, producing shock waves and high-pressure forces. These loads exert intense, short-duration forces on nearby structures, leading to potential damage such as deformation, cracking, or collapse. The magnitude of blast loads depends on factors like the explosion's energy, distance from the source, and the structure's geometry and material properties. They can also create dynamic effects, such as debris impact or air pressure oscillations. Proper design against blast loads is critical for ensuring safety in high-risk environments.

Impact
Impact loads occur when a sudden force is applied to a structure due to collisions or falling objects, leading to rapid stress and deformation. These loads can cause localized damage, cracks, or even catastrophic failure if the structure is not designed to absorb or dissipate the energy. The magnitude depends on the velocity, mass, and contact area of the impacting object. Impact loads are particularly dangerous because they can exceed the material's strength or create dynamic effects like vibrations. Proper design, including energy-absorbing materials and structural reinforcements, is essential to mitigate these risks.

Machinery vibrations
Wind loads are forces exerted by the movement of air on structures and objects, caused by atmospheric pressure differences due to temperature variations, weather systems, or geographical factors. These loads depend on wind speed, air density, and the shape, size, and orientation of the structure. Buildings, bridges, towers, and other exposed structures experience wind loads, which can lead to vibrations, deflections, or structural failure if not properly accounted for. Factors like turbulence, gusts, and aerodynamic effects, such as lift and drag, influence the magnitude and distribution of wind loads. In engineering, wind loads are analyzed using standards and simulations to ensure structures can withstand both static and dynamic wind effects.
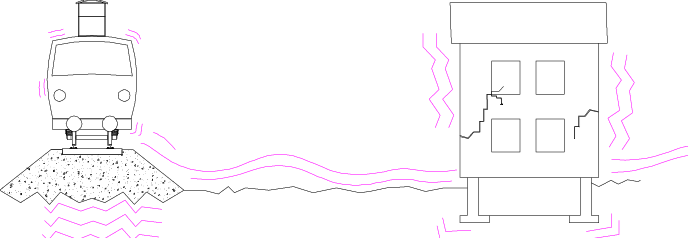
Traffic
Train traffic generates vibrations due to the dynamic interaction between the train, tracks, and underlying soil. These vibrations propagate through the ground, potentially affecting nearby structures and causing discomfort to occupants. The intensity depends on train speed, axle load, track conditions, and soil properties. Prolonged exposure to such vibrations can lead to structural fatigue, settlement, or resonance in buildings. Proper track design, damping systems, and vibration isolation measures are essential to minimize these effects and ensure safety and comfort. pact loads occur when a sudden force is applied to a structure due to collisions or falling objects, leading to rapid stress and deformation. These loads can cause localized damage, cracks, or even catastrophic failure if the structure is not designed to absorb or dissipate the energy. The magnitude depends on the velocity, mass, and contact area of the impacting object. Impact loads are particularly dangerous because they can exceed the material's strength or create dynamic effects like vibrations.
Methods for solving dynamic problems
The main methods and approaches for solving dynamic problems in engineering are:
- Modal analysis methods: linear problems
- Frequency field methods (complex variable): interaction problems
- Step-by-step methods (direct integration over time): non-linear problems
Modal analysis: natural frequencies and mode shapes
Modal analysis is a fundamental tool in dynamic calculations, as it provides a clear understanding of a structure or system's natural frequencies, mode shapes, and damping characteristics. These parameters are critical for predicting how a system responds to dynamic loads, such as vibrations, impacts, or oscillations.
By identifying the natural frequencies, engineers can avoid resonance, a phenomenon where external forces match a system's natural frequency, leading to excessive vibrations and potential failure.
Mode shapes give insight into how different parts of a structure move relative to each other during vibration, helping engineers design systems that distribute stresses effectively and avoid weak points.
Damping characteristics are essential for determining how quickly a system dissipates energy, which influences stability and long-term performance. Modal analysis is widely applied across industries, including aerospace, automotive, civil, and mechanical engineering. For example, it ensures the stability of bridges under wind loads, the safety of tall buildings during earthquakes, and the operational efficiency of machinery by minimizing vibration-induced wear and noise.
Advances in computational techniques, such as finite element analysis (FEA), have made modal analysis more accessible, allowing engineers to simulate complex systems accurately before physical testing. In essence, modal analysis is indispensable for optimizing designs, enhancing safety, and ensuring reliable performance in dynamic environments.
Linear dynamic analysis
Linear dynamic analysis is a method used in engineering to study the behavior of structures and systems subjected to time-varying forces or motions, assuming the relationship between applied loads and the system's response is linear. This means that deformations, displacements, and internal forces are directly proportional to the applied loads, and the material remains within its elastic range, without permanent deformation.

Linear dynamic analysis is a key aspect for understanding how structures respond to dynamic events such as vibrations, impacts, and seismic activity. It involves solving equations of motion that account for inertia, damping, and stiffness to predict the time-dependent response of a system.
This type of analysis is widely used because it simplifies complex dynamic problems while providing valuable insights into performance under dynamic loads. Its importance in engineering lies in ensuring safety, reliability, and efficiency in designs. For instance, in civil engineering, it helps assess how buildings or bridges react to earthquakes or wind loads. In mechanical engineering, it evaluates the vibrational behavior of rotating machinery, ensuring components do not fail due to fatigue or resonance.
While linear dynamic analysis is an approximation, its computational simplicity makes it a powerful and practical tool for early-stage design and decision-making, helping engineers identify potential issues and optimize performance in dynamic conditions.
Nonlinear dynamic analysis
Nonlinear dynamic analysis is a method used in engineering to study the behavior of structures and systems subjected to time-dependent forces or motions, where the response is not directly proportional to the applied loads.
Unlike linear dynamic analysis, it considers nonlinearities that arise from material properties, geometric configurations, or boundary conditions. Material nonlinearity occurs when a material's stress-strain relationship is no longer elastic, such as plastic deformation or cracking. Geometric nonlinearity accounts for large deformations, where assumptions of small displacements and rotations no longer hold, like in buckling or flexible structures. Nonlinear boundary conditions include contact, friction, or other constraints that change during loading.
Nonlinear dynamic analysis is essential for accurately predicting the behavior of systems under extreme or complex loading scenarios, such as earthquakes, blast loads, or impact forces.
This analysis requires solving more complex equations of motion, often using iterative numerical methods, making it computationally intensive compared to linear analysis. However, it provides a more realistic representation of how structures behave in real-world conditions, especially when linear assumptions break down. For example, in earthquake engineering, nonlinear analysis helps simulate the inelastic behavior of buildings, ensuring designs account for energy dissipation and collapse prevention.
While more demanding, nonlinear dynamic analysis is critical for assessing safety, performance, and failure mechanisms under challenging conditions, where linear approximations are insufficient.
The risks of dynamic resonance
Dynamic resonance is a dangerous phenomenon that occurs when the frequency of external forces matches the natural frequency of a structure or system, causing vibrations to amplify significantly. This amplification can lead to excessive stresses, fatigue, and even catastrophic failure in engineering systems.

Resonance is particularly hazardous because the vibrations can grow uncontrollably with relatively small external forces, making structures or components vulnerable to damage.
For example, bridges exposed to rhythmic forces, like wind or footsteps, may collapse due to resonance, as seen in historical failures like the Tacoma Narrows Bridge. In machinery, resonance can cause severe wear, noise, and operational inefficiency.
Avoiding resonance is crucial to ensuring safety, reliability, and durability. Engineers achieve this by modifying natural frequencies, adding damping, or designing systems to operate outside resonant conditions. Identifying and mitigating resonance is a key aspect of dynamic analysis and critical for preventing catastrophic failures in real-world applications.
